从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数杭州市某某自动化科技服务中心之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂杭州市某某自动化科技服务中心起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:知识)
-
 10月25日,东莞市大岭山森林公园发布《关于禁止到公园未开发未开放区域开展户外活动的通告》,严禁组织旅游团前往森林公园未开发、未对社会开放的“网红”区域开展旅游活动。 东莞市大岭山森林公园属于自然公
...[详细]
10月25日,东莞市大岭山森林公园发布《关于禁止到公园未开发未开放区域开展户外活动的通告》,严禁组织旅游团前往森林公园未开发、未对社会开放的“网红”区域开展旅游活动。 东莞市大岭山森林公园属于自然公
...[详细]
-
 上半年全球电影市场一般都是波澜不惊。如果最近非要找一部充满娱乐精神的电影,那么《破墓》算是不错的选择。《破墓》自2月于韩国上映,商业表现颇为亮眼,成了韩国本年度首部观影人次突破千万的大卖之作。考虑到本
...[详细]
上半年全球电影市场一般都是波澜不惊。如果最近非要找一部充满娱乐精神的电影,那么《破墓》算是不错的选择。《破墓》自2月于韩国上映,商业表现颇为亮眼,成了韩国本年度首部观影人次突破千万的大卖之作。考虑到本
...[详细]
-
 5月4日,以“新时代 新汽车”为主题的2024第十八届)北京国际汽车展览会简称2024北京车展),在中国国际展览中心顺义馆闭幕。 主办方提供的数字显示,共有13个国家近500家企业参展。10天展
...[详细]
5月4日,以“新时代 新汽车”为主题的2024第十八届)北京国际汽车展览会简称2024北京车展),在中国国际展览中心顺义馆闭幕。 主办方提供的数字显示,共有13个国家近500家企业参展。10天展
...[详细]
-
 2024中关村论坛年会期间,中关村展示中心常设展重装亮相,展览以“四个面向”为主线,展示一系列前沿科技,带来诸多惊喜。世界目光再次聚焦中关村——“创新:建设更加美好的世界”。 在面向世界科技
...[详细]
2024中关村论坛年会期间,中关村展示中心常设展重装亮相,展览以“四个面向”为主线,展示一系列前沿科技,带来诸多惊喜。世界目光再次聚焦中关村——“创新:建设更加美好的世界”。 在面向世界科技
...[详细]
-
 当地时间10月26日,美国国防部发布声明表示,美国国防部长奥斯汀当日与以色列国防部长加兰特进行通话,讨论以色列国防军对伊朗军事目标实施的精确打击。 声明表示,奥斯汀重申了美国对以色列安全的承诺。
...[详细]
当地时间10月26日,美国国防部发布声明表示,美国国防部长奥斯汀当日与以色列国防部长加兰特进行通话,讨论以色列国防军对伊朗军事目标实施的精确打击。 声明表示,奥斯汀重申了美国对以色列安全的承诺。
...[详细]
-
 置身北京的中国非物质文化遗产馆中,观赏工艺美术家的敦煌图案手稿;到刚刚开馆的西藏非物质文化遗产博物馆中,近距离感受绚丽多彩的唐卡、美观实用的织造技艺;在位于江苏的六朝博物馆里,穿着汉服制作一把漂漆扇…
...[详细]
置身北京的中国非物质文化遗产馆中,观赏工艺美术家的敦煌图案手稿;到刚刚开馆的西藏非物质文化遗产博物馆中,近距离感受绚丽多彩的唐卡、美观实用的织造技艺;在位于江苏的六朝博物馆里,穿着汉服制作一把漂漆扇…
...[详细]
-
 “每天滴一次,就可以延缓儿童近视”,“效果立竿见影,比OK镜好使”,“睡前滴一滴,半年没涨度数”......过去几年,不少家长将阿托品当作“近视神药”。即便之前还未在中国大陆地区获批上市,阿托品就凭借
...[详细]
“每天滴一次,就可以延缓儿童近视”,“效果立竿见影,比OK镜好使”,“睡前滴一滴,半年没涨度数”......过去几年,不少家长将阿托品当作“近视神药”。即便之前还未在中国大陆地区获批上市,阿托品就凭借
...[详细]
-
 近日,国家野外科学观测研究站观测技术规范宣贯与应用研讨会在中国科学院地理科学与资源研究所举办。会上发布了国家野外站观测技术规范研究编制工作的首个阶段性成果—《国家野外科学观测研究站观测技术规范 第一卷
...[详细]
近日,国家野外科学观测研究站观测技术规范宣贯与应用研讨会在中国科学院地理科学与资源研究所举办。会上发布了国家野外站观测技术规范研究编制工作的首个阶段性成果—《国家野外科学观测研究站观测技术规范 第一卷
...[详细]
-
 “每天都有自习室品牌入驻,每个月都有自习室倒下撤出……”今天实地走访了郑州几家自习室,在曾经的教培圣地——凯旋门。我记得这里一楼大厅墙壁上堆满了各种教培的广告,如今全部不见了,一楼就只保留了一家合规的
...[详细]
“每天都有自习室品牌入驻,每个月都有自习室倒下撤出……”今天实地走访了郑州几家自习室,在曾经的教培圣地——凯旋门。我记得这里一楼大厅墙壁上堆满了各种教培的广告,如今全部不见了,一楼就只保留了一家合规的
...[详细]
-
 5月1日上午,中国海军福建舰出海开展首次航行试验。 2022年6月17日,我国第三艘航空母舰下水命名仪式举行,经中央军委批准,我国第三艘航空母舰命名为“中国人民解放军海军福建舰”,舷号为“18”
...[详细]
5月1日上午,中国海军福建舰出海开展首次航行试验。 2022年6月17日,我国第三艘航空母舰下水命名仪式举行,经中央军委批准,我国第三艘航空母舰命名为“中国人民解放军海军福建舰”,舷号为“18”
...[详细]

 神十九航天员乘组计划于明年4月下旬或5月上旬返回
神十九航天员乘组计划于明年4月下旬或5月上旬返回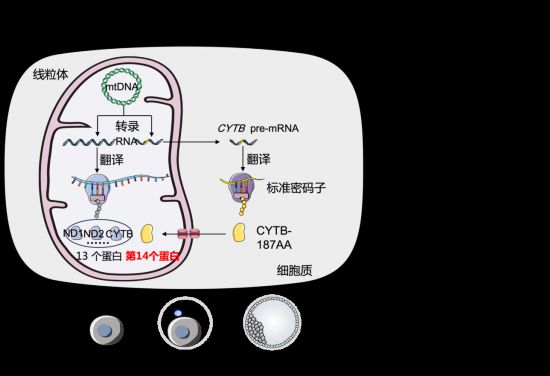 我国科学家首次发现线粒体基因编码第14个蛋白质
我国科学家首次发现线粒体基因编码第14个蛋白质 “良田”不只在田野(快评)
“良田”不只在田野(快评) “含金量”“含新量”不断提升 中国经济新动能加速形成
“含金量”“含新量”不断提升 中国经济新动能加速形成 航天员宋令东将是我国首个飞天的“90后”男航天员
航天员宋令东将是我国首个飞天的“90后”男航天员
